TEOREMA DEL VALOR MEDIO 

En cálculo diferencial, el teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante del cálculo. El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para demostrar  otros teoremas. El teorema de valor medio puede usarse para demostrar el TEOREMA DE TAYLOR ya que es un caso especial.

 

ENUNCIADO PARA UNA VARIABLE 

En esencia el teorema dice que dada cualquier función f continua en el intervalo [a, b] y diferenciable en el intervalo abierto (a, b) entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es paralela a la recta secante que une los puntos (a, f(a)) y (b, f(b)). Es decir:

 

Este teorema lo formuló Lagrange.

El teorema del valor medio de Lagrange de hecho es una generalización del teorema de roll que dice que si una función es definida y continua [a, b], diferenciable en el intervalo abierto (a, b), y toma valores iguales en los extremos del intervalo – en otras palabras, f(a) = f(b) – entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es horizontal, es decir f'(c) = 0.

 

    \frac{f(b) - f(a)}{b-a} = f ' (c)

 

Este teorema lo formuló Lagrange.

El teorema del valor medio de Lagrange de hecho es una generalización del teorema de Rolle que dice que si una función es definida y continua [a, b], diferenciable en el intervalo abierto (a, b), y toma valores iguales en los extremos del intervalo – en otras palabras, f(a) = f(b) – entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es horizontal, es decir f'(c) = 0.

 

Demostración

1) Primero se consideran dos puntos (a,f(a))\; y (b,f(b))\; pertenecientes al gráfico de la función. La ecuación de la recta que pasa por estos dos puntos es:

y = f(a) + \frac{f(b)-f(a)}{b-a}(x-a)

Se define una función auxiliar:

g(x) = f(x) - y = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a}(x-a) \right ]

Puesto que f es continua en [a, b] y diferenciable en (a, b), lo mismo se puede decir de g. Además g satisface las condiciones del Teorema de Roll en [a,b] ya que:

g(a) = f(a) - f(a) - \frac{f(b)-f(a)}{b-a}(a-a) = 0 = g(b)= f(b) - f(a) - \frac{f(b)-f(a)}{b-a}(b-a)

Por el Teorema de Rolle, como g es derivable en (a, b) y g(a) = g(b), existe un c perteneciente (a, b) tal que g'(c) = 0, y por tanto:

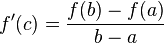
0 = g ' (c) = f ' (c) - \frac{f(b)-f(a)}{b - a}

y así

f ' (c) = \frac{f(b)-f(a)}{b-a}

que es lo que se quería demostrar.

2) Sea a m_{ab} la pendiente de la recta secante entre [a,b], se define la ecuación punto-pendiente:

y = m_{ab}x+c_1

m_{ab}=\frac{f(b)-f(a)}{b-a}

o también,

-m_{ab}x + y = c_1

De acuerdo al enunciado la función es derivable en (a,b), por lo que se puede escoger algún valor  x=c en dicho intervalo tal que  f'(c) existe y es la pendiente de la recta tangente en dicho punto y por ende la recta tangente tiene la forma (punto-pendiente):

y = f'(c)x+c_2

o también,

-f'(c)x + y = c_2

Se observa que se llega a un sistema lineal de 2x2

\left \{ \begin{matrix} -m_{ab}x + y = c_1 \\ -f'(c)x + y = c_2 \end{matrix} \right .

La matriz del sistema es:

\mathbb{A} = \; \begin{pmatrix} -m_{ab} & 1 \\ -f'(c) & 1 \\ \end{pmatrix}

Y su determinante es:

det(A) = f'(c)- m_{ab}

Para que el sistema no tenga solución se debe cumplir det(A)=0, por lo tanto las rectas son paraleas en x=c, es decir f'(c) = mab

Entonces, existe al menos un punto que no da solución al sistema y además la recta tangente al mismo es paralela a la recta entre a y b, es decir:

f'(c)=m_{ab}

o también,

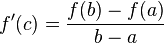
f ' (c) = \frac{f(b)-f(a)}{b-a}

Con ello queda demostrado el teorema del valor medio.

 

 

Para la gente interesada en el Valor Medio

Esta página web fue creada para dar a enterder por medio electronico los conocimiendos del valor medio con un contexto novedoso e intereante para que las personas se interesen en el y no lo olviden, como suele suceder con alumnos. 

Como objetivo principal tenemos crear una grata, clara e interesante informacion.

 

 

 

 

Ejercicios

Ejemplos

30.05.2015 21:17
Ejemplo ¿Se puede aplicar el teorema de Lagrange a f(x) = x3 en [−1, 2]? f(x) es continua en [−1, 2] y derivable en (−1, 2) por tanto se puede aplicar el teorema del valor medio: teorema del valor medio solución    

Ejercicios sobre el valor medio

30.05.2015 21:01
1 ¿Es aplicable el teorema de Rolle a la función f(x) = |x − 1| en el intervalo [0, 2]? 2 Estudiar si la función f(x) = x − x3 satisface las condiciones del teorema de Rolle en los intervalos [−1, 0] y [0, 1]. en caso afirmativo determinar los valores de c. 3 ¿Satisface la función f(x) = 1 − x las...